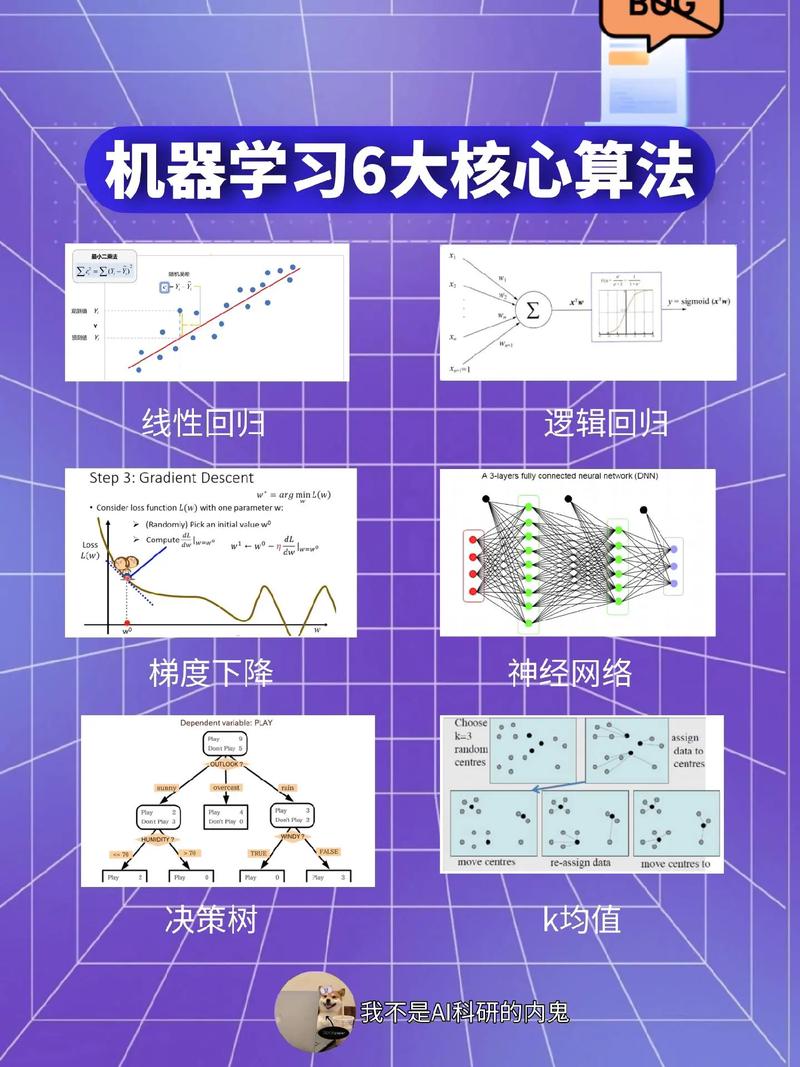
机器学习中的贝叶斯方法是一种利用贝叶斯定理来构建统计模型的方法。贝叶斯定理描述了在给定一些观测数据的情况下,如何计算一个假设或参数的概率。在机器学习中,贝叶斯方法通常用于以下方面:
1. 参数估计:贝叶斯方法可以用于估计模型参数的分布,而不是仅仅估计参数的点估计值。这允许模型的不确定性被纳入考虑,并且可以提供参数估计的置信区间。
2. 模型选择:贝叶斯方法可以用于比较不同模型,通过计算每个模型的边际似然(即模型在所有可能参数值下的平均似然)来进行。这有助于选择最适合数据的模型。
3. 预测:在贝叶斯框架下,预测可以基于模型的参数分布进行,而不是基于参数的单个估计值。这提供了预测的不确定性度量。
4. 分类:贝叶斯分类器,如朴素贝叶斯分类器,是基于贝叶斯定理来对数据进行分类的。这些分类器假设特征之间是条件独立的,这在某些情况下是一个强大的假设。
5. 回归:贝叶斯回归方法,如贝叶斯线性回归,可以用于预测连续变量。这些方法可以提供对预测结果的概率分布估计。
6. 无监督学习:贝叶斯方法也适用于无监督学习任务,如聚类和密度估计。在这些任务中,贝叶斯方法可以帮助识别数据中的潜在结构。
贝叶斯方法的一个关键优势是它们能够自然地处理不确定性,并允许模型随着新数据的到来而更新。它们也可能面临计算上的挑战,因为需要处理高维参数空间中的积分和优化问题。为了克服这些挑战,人们开发了各种近似方法,如变分贝叶斯和马尔可夫链蒙特卡罗方法。
深入解析机器学习中的贝叶斯方法
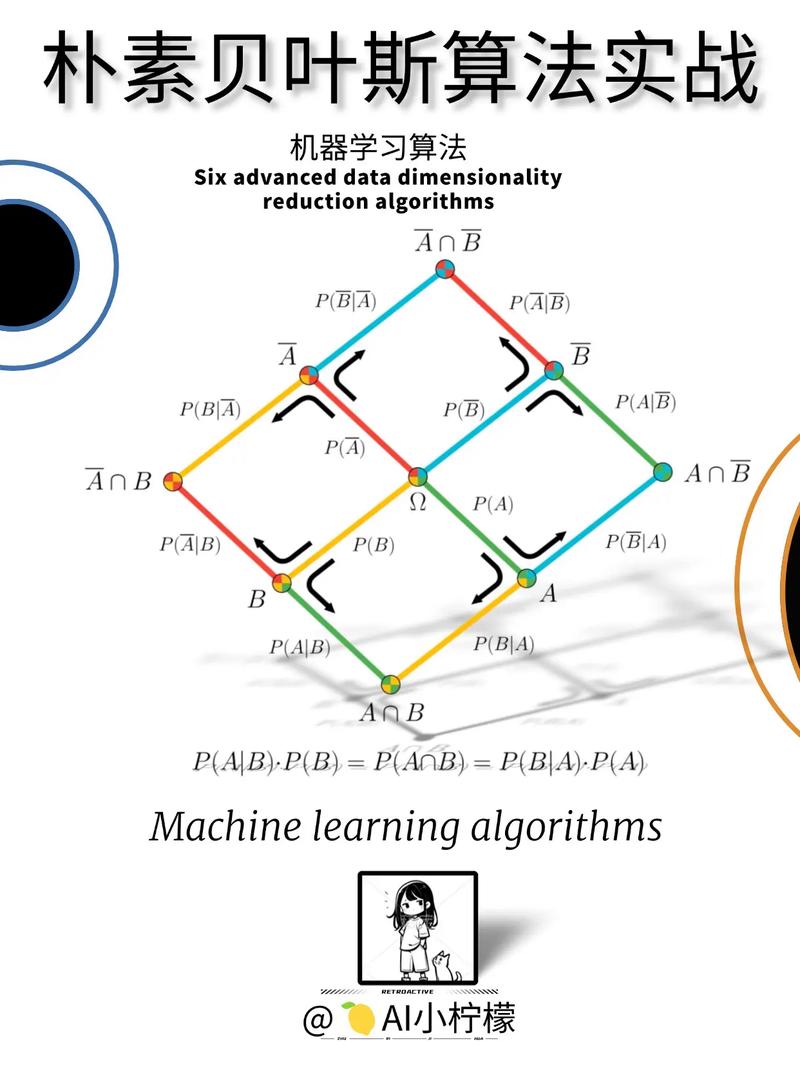
一、贝叶斯方法的原理
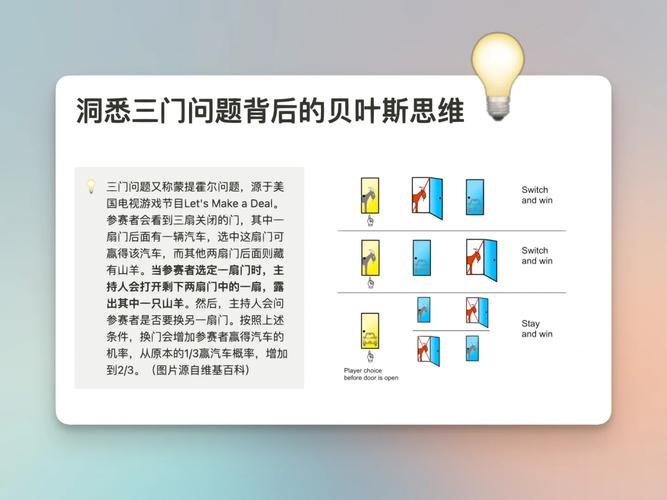
贝叶斯方法是一种基于贝叶斯定理的概率推理方法。贝叶斯定理描述了已知某个事件发生的情况下,另一个事件发生的概率如何计算。在机器学习中,贝叶斯方法主要用于处理不确定性问题,通过先验知识和观测数据来推断未知量。
二、贝叶斯方法在机器学习中的应用

1. 朴素贝叶斯分类器
朴素贝叶斯分类器是一种基于贝叶斯定理的分类算法,它假设特征之间相互独立。朴素贝叶斯分类器在文本分类、垃圾邮件过滤等领域有着广泛的应用。
2. 贝叶斯网络
贝叶斯网络是一种图形化的概率模型,它通过有向无环图(DAG)来表示变量之间的依赖关系。贝叶斯网络在基因分析、故障诊断等领域有着重要的应用。
3. 贝叶斯优化
贝叶斯优化是一种基于贝叶斯方法的优化算法,它通过构建目标函数的概率模型来寻找最优参数。贝叶斯优化在超参数优化、模型选择等领域有着广泛的应用。
三、贝叶斯方法的优势

1. 处理不确定性问题
贝叶斯方法能够处理不确定性问题,通过先验知识和观测数据来推断未知量,从而提高模型的鲁棒性。
2. 参数估计
贝叶斯方法能够对模型参数进行估计,从而提高模型的预测精度。
3. 模型选择
贝叶斯方法能够根据观测数据选择最优模型,从而提高模型的泛化能力。
四、贝叶斯方法的挑战
1. 计算复杂度
贝叶斯方法通常需要计算大量的概率分布,这可能导致计算复杂度较高。
2. 先验知识的选择
贝叶斯方法需要先验知识来构建概率模型,而先验知识的选择可能会对模型的性能产生较大影响。
五、实际应用案例
1. 医学检测
贝叶斯方法在医学检测领域有着广泛的应用,如疾病诊断、药物疗效评估等。通过贝叶斯方法,可以结合医生的经验和患者的观测数据,提高诊断的准确性。
2. 金融风控
贝叶斯方法在金融风控领域也有着重要的应用,如信用评分、欺诈检测等。通过贝叶斯方法,可以分析客户的信用风险,从而降低金融风险。
3. 自然语言处理
贝叶斯方法在自然语言处理领域也有着广泛的应用,如文本分类、情感分析等。通过贝叶斯方法,可以分析文本数据,提高文本处理的准确性和效率。
贝叶斯方法在机器学习领域中的应用越来越广泛,它能够处理不确定性问题、进行参数估计和模型选择。贝叶斯方法也存在计算复杂度和先验知识选择等挑战。在实际应用中,我们需要根据具体问题选择合适的贝叶斯方法,以提高模型的性能。