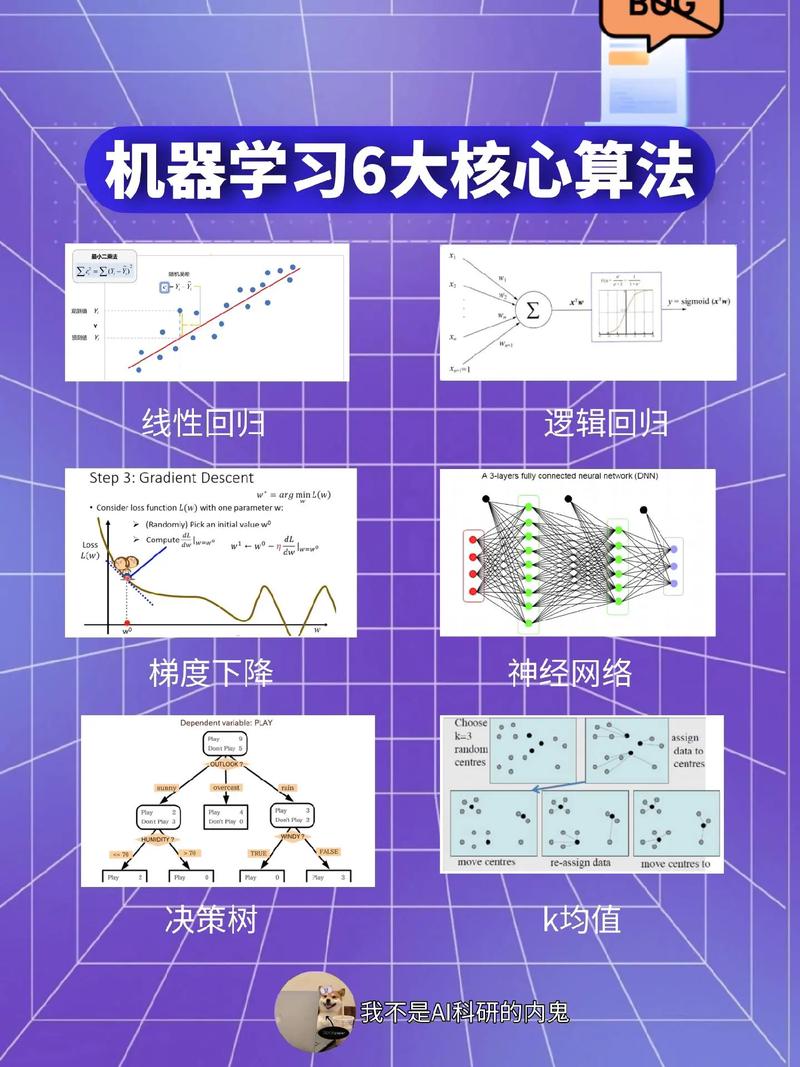
机器学习中的数学基础主要包括以下几个方面:
1. 线性代数:线性代数是机器学习的基础,主要涉及向量、矩阵、特征值和特征向量等概念。在机器学习中,线性代数被广泛应用于数据的表示、模型的构建和优化等环节。2. 概率论与统计学:概率论与统计学是机器学习的重要工具,用于描述数据的分布、估计参数和评估模型的性能等。在机器学习中,概率论与统计学被广泛应用于监督学习、无监督学习和强化学习等算法中。3. 微积分:微积分是机器学习中优化算法的基础,主要涉及导数、积分和极限等概念。在机器学习中,微积分被广泛应用于模型的优化和参数的调整等环节。4. 最优化理论:最优化理论是机器学习中的重要工具,用于求解模型的最优解。在机器学习中,最优化理论被广泛应用于线性回归、支持向量机和神经网络等算法中。5. 信息论:信息论是机器学习中的重要工具,用于描述数据的不确定性和信息量。在机器学习中,信息论被广泛应用于特征选择、模型评估和信息传递等环节。
以上是机器学习中的数学基础,对于想要深入学习机器学习的人来说,掌握这些数学知识是非常重要的。
机器学习中的数学基础:构建智能算法的基石

一、线性代数:数据表示与运算的利器

线性代数是机器学习中的基础数学工具,它主要研究向量、矩阵及其运算。在机器学习中,数据通常以矩阵或向量形式表示,因此线性代数在数据表示和运算方面发挥着重要作用。
1. 向量:向量是线性代数的基本概念之一,可以看作一组有序数值的集合,用于描述对象的特征。例如,一个人的身高、体重和年龄可以组成一个三维向量。
2. 矩阵:矩阵是由一系列数字组成的二维数组,可以表示数据之间的关系。在机器学习中,矩阵常用于表示数据集、特征和模型参数等。
3. 矩阵运算:矩阵运算包括矩阵加法、减法、乘法、转置等。这些运算在机器学习中用于数据预处理、特征提取、模型构建等环节。
二、概率论与数理统计:理解数据分布与模型预测

概率论与数理统计是机器学习中的另一项重要数学基础,它们帮助我们理解数据分布、模型预测和参数估计等问题。
1. 概率论:概率论研究随机事件及其概率。在机器学习中,概率论用于描述数据的不确定性、模型预测的可靠性等。
2. 数理统计:数理统计研究数据的收集、处理和分析。在机器学习中,数理统计用于数据预处理、特征选择、模型评估等环节。
3. 常用统计量:均值、方差、协方差等统计量用于描述数据的集中趋势、离散程度和相关性。
三、微积分:优化模型参数的利器
微积分是机器学习中的另一项重要数学基础,它主要研究函数、极限、导数和积分等概念。在机器学习中,微积分用于优化模型参数、求解最优化问题等。
1. 导数:导数表示函数在某一点的斜率,用于求解最优化问题。在机器学习中,导数常用于梯度下降算法中计算损失函数的梯度。
2. 积分:积分表示函数在某个区间内的累积值,用于计算概率密度函数、求解微分方程等。
四、编程语言:实现机器学习算法的工具
编程语言是机器学习算法实现的重要工具。Python、R、MATLAB等编程语言在机器学习领域应用广泛。
1. Python:Python是一种易于学习、功能强大的编程语言,拥有丰富的机器学习库,如scikit-learn、TensorFlow、PyTorch等。
2. R:R是一种专门用于统计分析和图形绘制的编程语言,拥有强大的统计建模和机器学习功能。
3. MATLAB:MATLAB是一种高性能的数值计算和可视化工具,在工程和科学领域应用广泛。
机器学习中的数学基础是构建智能算法的基石。掌握线性代数、概率论与数理统计、微积分等数学知识,有助于我们更好地理解机器学习算法,提高算法性能。同时,熟练掌握编程语言是实现机器学习算法的关键。通过不断学习和实践,我们可以为人工智能领域的发展贡献自己的力量。