机器学习和数学是密切相关的领域。在机器学习中,数学是构建和训练模型的基础,是理解和分析模型性能的关键工具。以下是机器学习与数学之间的一些主要联系:
1. 线性代数:线性代数是机器学习的基础,因为它提供了处理多维数据的方法。向量、矩阵和线性变换是线性代数的关键概念,它们在机器学习中用于表示数据、构建模型和进行计算。
2. 概率论和统计学:概率论和统计学是理解数据不确定性和随机性的关键。在机器学习中,这些概念用于构建模型、估计参数、评估模型性能和进行预测。
3. 微积分:微积分在机器学习中用于优化模型参数。梯度下降是一种常用的优化算法,它基于微积分中的导数概念。
4. 概率图模型:概率图模型是一种强大的工具,用于表示和推理复杂概率关系。它们在机器学习中用于构建复杂模型,如贝叶斯网络和马尔可夫链。
5. 最优化理论:最优化理论是机器学习中的一个重要分支,它关注于找到函数的最大值或最小值。最优化算法,如梯度下降和随机梯度下降,用于训练机器学习模型。
6. 信息论:信息论是研究信息传递和编码的理论。在机器学习中,信息论用于评估模型的复杂性和信息增益。
7. 数值分析:数值分析是研究数值方法和算法的理论。在机器学习中,数值分析用于实现和优化算法,如求解线性方程组和优化问题。
8. 逻辑和集合论:逻辑和集合论是数学的基础,它们在机器学习中用于表示和推理知识。例如,逻辑回归是一种基于逻辑的机器学习算法。
9. 几何学:几何学在机器学习中用于处理空间数据,如图像和视频。几何学概念,如距离、形状和变换,在机器学习中用于特征提取和模型构建。
10. 拓扑学:拓扑学是研究空间结构和性质的理论。在机器学习中,拓扑学用于分析数据结构和识别模式。
总之,数学是机器学习的基础,它提供了构建、训练和分析模型所需的工具和方法。对于想要深入理解机器学习的人来说,掌握数学知识是非常重要的。
机器学习中的数学基础:探索数据与算法的桥梁
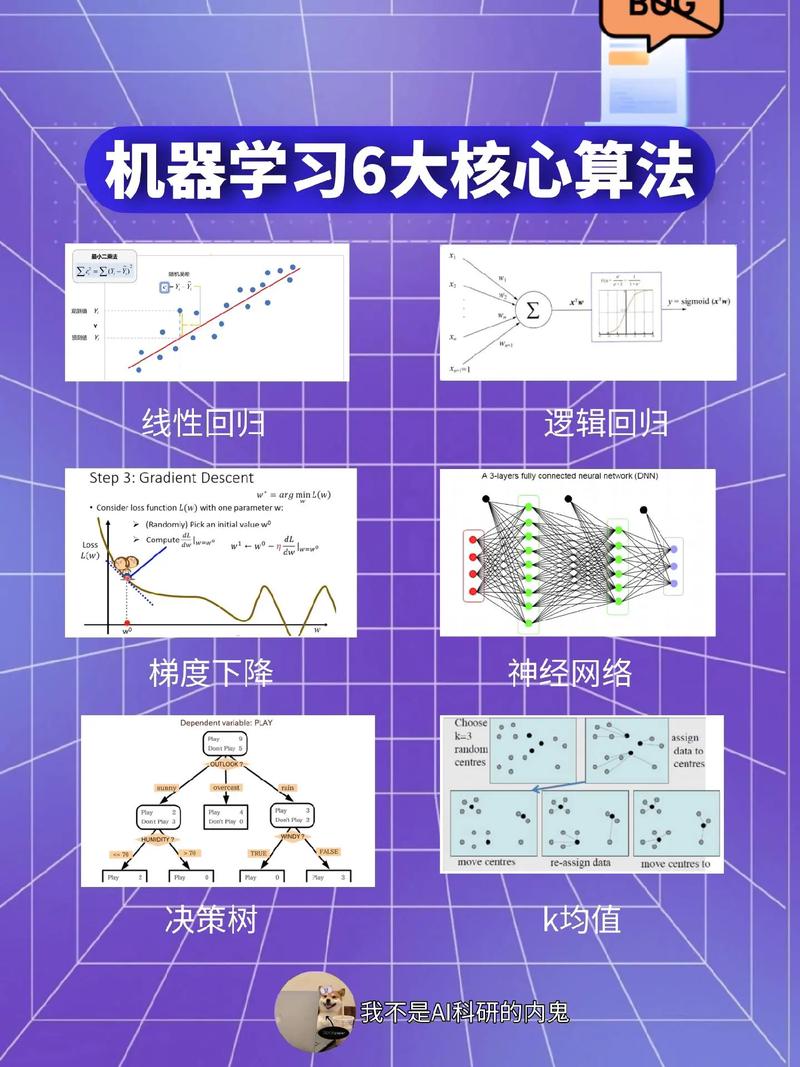
概率论与数理统计:机器学习的基石

概率论和数理统计是机器学习中的两大基石。概率论为机器学习提供了描述不确定性的语言,而数理统计则提供了从数据中提取信息的方法。
在机器学习中,概率论用于描述数据分布、模型参数的先验分布以及预测结果的置信度。例如,贝叶斯定理是概率论在机器学习中的一个重要应用,它可以帮助我们根据先验知识和观测数据更新模型参数的信念。
数理统计则提供了从样本数据中估计总体参数的方法。例如,假设检验、置信区间和假设检验等统计方法可以帮助我们判断模型是否具有统计显著性。
线性代数:矩阵与向量的世界

线性代数是机器学习中不可或缺的工具,它涉及到矩阵、向量、线性变换等概念。在机器学习中,线性代数被广泛应用于特征提取、降维、优化等方面。
矩阵和向量是线性代数中的基本概念,它们在机器学习中扮演着重要角色。例如,在主成分分析(PCA)中,通过求解协方差矩阵的特征值和特征向量,可以实现对数据的降维。
线性变换是线性代数中的另一个重要概念,它可以将数据从一种表示形式转换为另一种表示形式。例如,在神经网络中,权重矩阵和偏置向量构成了线性变换,它们决定了输入数据在神经网络中的传播方式。
优化理论:寻找最优解的旅程
优化理论是机器学习中解决优化问题的核心工具。在机器学习中,优化问题通常涉及到寻找模型参数的最优值,以实现预测或分类的准确性。
优化理论提供了多种算法来解决优化问题,如梯度下降、牛顿法、共轭梯度法等。这些算法通过迭代更新模型参数,逐步逼近最优解。
在机器学习中,优化问题通常与损失函数相关联。损失函数用于衡量模型预测结果与真实值之间的差异,优化算法的目标是找到使损失函数最小的模型参数。
信息论:数据与知识的度量
信息论是研究信息传输、存储和处理的理论。在机器学习中,信息论提供了度量数据复杂性和信息量的方法,有助于我们理解数据背后的规律。
信息熵是信息论中的一个重要概念,它用于衡量数据的随机性和不确定性。在机器学习中,信息熵可以帮助我们选择合适的特征,以降低模型的复杂性和提高预测准确性。
互信息是另一个重要的信息论概念,它用于衡量两个变量之间的相关性。在机器学习中,互信息可以帮助我们识别数据中的潜在关系,从而提高模型的性能。
数学作为机器学习的基础,为算法提供了坚实的理论基础和强大的工具。从概率论和数理统计到线性代数、优化理论和信息论,数学在机器学习中扮演着不可或缺的角色。随着机器学习技术的不断发展,数学在机器学习中的应用将更加广泛和深入。