机器学习数学函数,基础与重要性

1. 线性函数：f = ax b，其中a和b是常数。线性函数常用于线性回归模型中，表示自变量x和因变量y之间的线性关系。

2. 指数函数：f = a^x，其中a是常数。指数函数常用于描述指数增长或衰减现象，如人口增长、放射性衰变等。

3. 对数函数：f = log，其中log表示以10为底的对数。对数函数常用于将数据压缩到更小的范围内，便于处理和可视化。

4. 指数和对数函数的组合：f = a^x b log，这种组合函数常用于描述复杂的现象，如生物种群的增长。

5. Sigmoid函数：f = 1 / qwe2，其中e是自然对数的底数。Sigmoid函数常用于二分类问题中，将线性函数的输出压缩到0到1之间，表示概率。

6. 双曲正切函数：f = tanh，其中tanh表示双曲正切函数。双曲正切函数常用于多分类问题中，将线性函数的输出压缩到1到1之间，表示概率。

7. Softmax函数：f = exp / sumqwe2，其中exp表示自然指数函数。Softmax函数常用于多分类问题中，将线性函数的输出转换为概率分布。

8. 损失函数：损失函数用于衡量模型预测值与真实值之间的差异，如均方误差（MSE）、交叉熵损失等。损失函数的优化是机器学习模型训练的关键。

9. 梯度函数：梯度函数用于计算损失函数关于模型参数的偏导数，如梯度下降法中使用的梯度。梯度函数的求解是优化算法的核心。

10. 激活函数：激活函数用于引入非线性特性，提高模型的拟合能力。常见的激活函数有ReLU、Sigmoid、Tanh等。

11. 正则化项：正则化项用于防止模型过拟合，如L1正则化、L2正则化等。正则化项的引入可以提高模型的泛化能力。

12. 概率密度函数：概率密度函数用于描述随机变量的分布，如高斯分布、伯努利分布等。概率密度函数在贝叶斯推断、隐马尔可夫模型等场景中具有重要作用。

13. 特征选择函数：特征选择函数用于从原始特征中选择对模型预测能力贡献最大的特征子集，如信息增益、卡方检验等。特征选择函数可以提高模型的效率和准确性。

14. 距离函数：距离函数用于衡量两个数据点之间的相似度，如欧氏距离、余弦相似度等。距离函数在聚类、推荐系统等场景中具有重要作用。

15. 优化算法中的数学函数：如梯度下降法中的学习率、动量等，这些函数用于控制优化过程，提高模型的训练速度和稳定性。

这些数学函数在机器学习中的具体应用可能因模型和算法的不同而有所差异。了解这些函数的基本原理和特点，有助于更好地理解和应用机器学习技术。

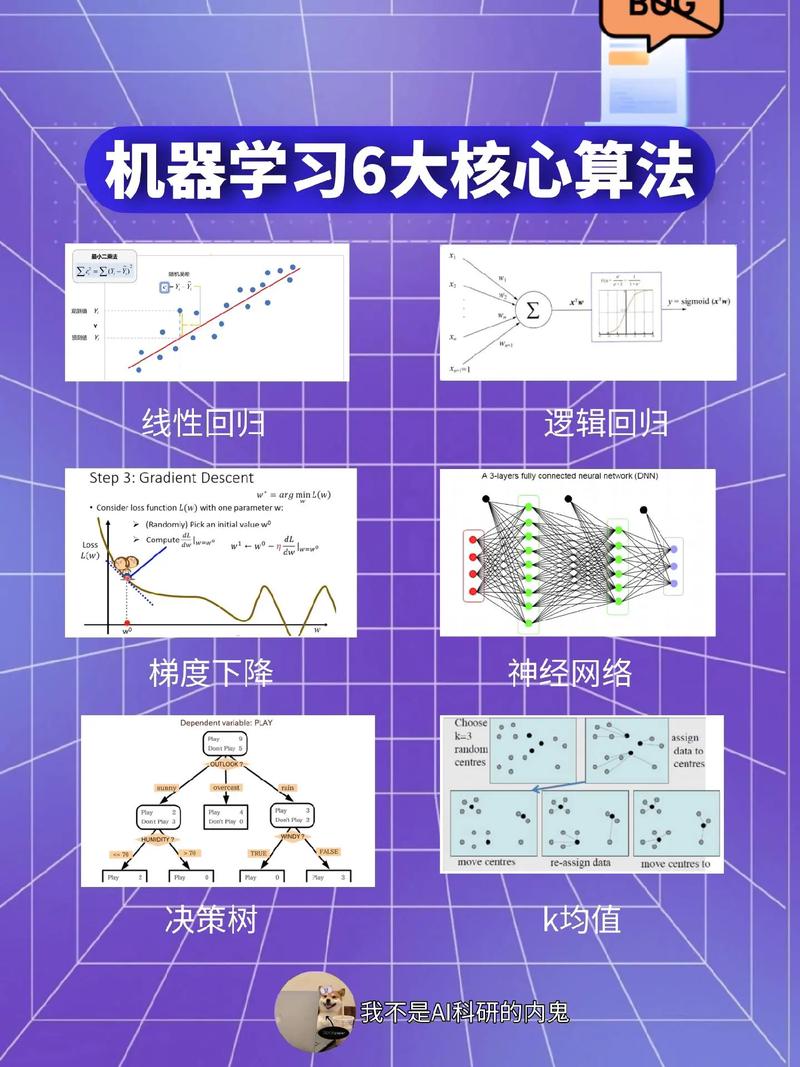
机器学习作为人工智能的一个重要分支，其核心在于通过算法从数据中学习并做出预测或决策。在这个过程中，数学函数扮演着至关重要的角色。本文将探讨机器学习中常用的数学函数及其重要性。

矩阵乘法：用于计算两个矩阵的乘积，是机器学习中矩阵运算的基础。

矩阵求逆：用于求解线性方程组，是优化算法中的重要步骤。

特征值和特征向量：用于降维和特征提取，有助于提高模型的性能。

向量化：将多个变量合并成一个向量，便于进行矩阵运算。

概率分布：描述随机变量可能取值的概率，如正态分布、伯努利分布等。

期望值：描述随机变量的平均值，是评估模型性能的重要指标。

方差：描述随机变量的离散程度，有助于了解数据的波动性。

协方差：描述两个随机变量之间的关系，是特征选择和降维的重要依据。

sigmoid函数：将输入值压缩到0和1之间，常用于二分类问题。

ReLU函数：非线性激活函数，有助于提高神经网络的性能。

Softmax函数：将输入值转换为概率分布，常用于多分类问题。

均方误差（MSE）：用于回归问题，衡量预测值与真实值之间的差异。

交叉熵损失（Cross-Entropy Loss）：用于分类问题，衡量预测概率与真实概率之间的差异。

Huber损失：对异常值具有鲁棒性，适用于数据中存在噪声的情况。

梯度下降（Gradient Descent）：通过迭代更新模型参数，以最小化损失函数。

Adam优化器：结合了动量和自适应学习率，适用于大规模数据集。

SGD（Stochastic Gradient Descent）：随机梯度下降，适用于小批量数据。

机器学习中的数学函数是构建高效模型的关键。掌握这些函数有助于我们更好地理解机器学习算法的原理，并提高模型的性能。在学习和应用机器学习的过程中，不断探索和掌握这些数学函数，将有助于我们在人工智能领域取得更大的突破。