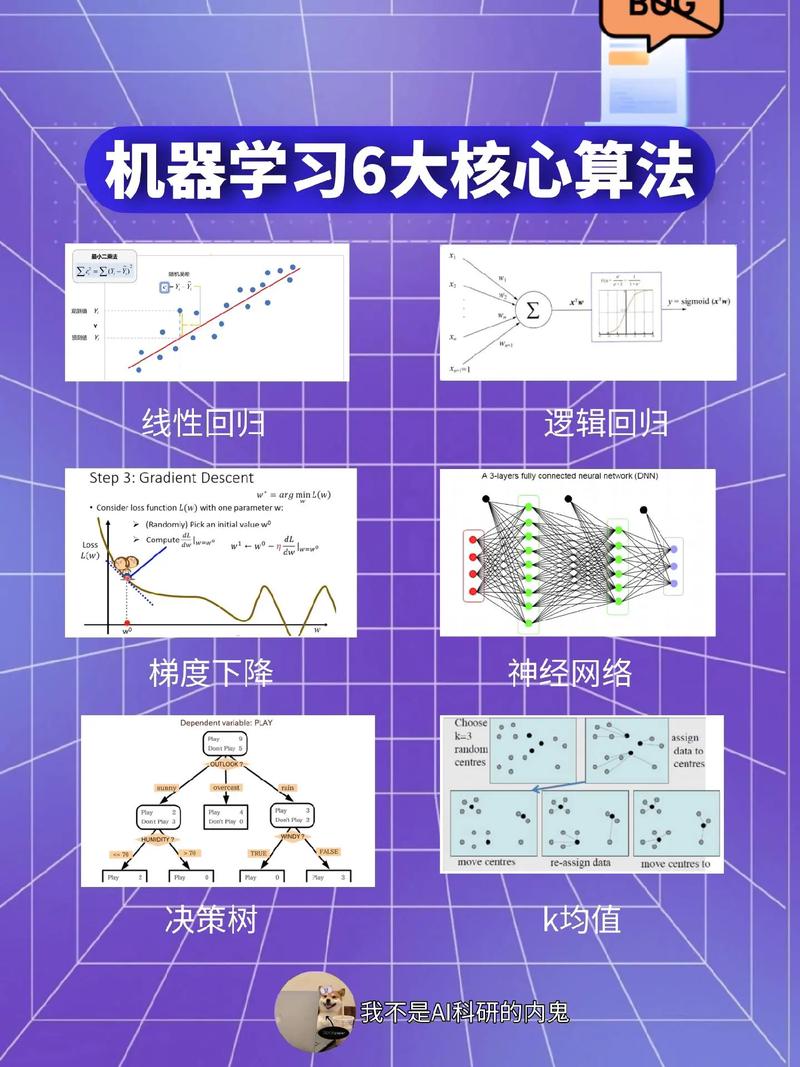
机器学习中的决策树是一种非常流行的监督学习算法,它通过一系列规则对数据进行分类或回归。决策树的核心思想是将数据集递归地划分为越来越小的子集,直到每个子集都足够纯,即它们中的大多数数据都属于同一个类别或具有相似的值。
决策树的基本组成部分:
决策树的构建:
决策树是通过选择最佳的属性来划分数据集,以便最大化数据集的纯度。常用的纯度度量包括信息增益(Information Gain)、增益率(Gain Ratio)和基尼指数(Gini Index)。这些度量帮助确定在给定节点上哪个属性是最优的划分标准。
1. 选择最佳划分属性:使用纯度度量来选择能够最好地将数据集分为两个子集的属性。2. 划分数据集:根据选定的属性值,将数据集划分为两个子集。3. 递归构建:对每个子集重复上述过程,直到满足停止条件(例如,节点包含的数据点足够少,或者所有数据点都属于同一类别)。
决策树的剪枝:
由于决策树可能会过度拟合训练数据,即它们会学习到数据中的噪声和异常点,因此通常需要对决策树进行剪枝(Pruning)来防止过拟合。剪枝可以通过预剪枝(在构建过程中进行)或后剪枝(在树构建完成后进行)来实现。
决策树的优势:
易于理解和解释:决策树的结果可以用树状图的形式表示,易于理解。 不需要数据预处理:决策树不需要对数据进行归一化或标准化处理。 适用于各种数据类型:决策树可以处理连续值和离散值数据。
决策树的局限性:
容易过拟合:决策树可能会学习到数据中的噪声和异常点,导致过拟合。 对缺失值敏感:决策树在处理包含缺失值的数据时可能会遇到问题。 对连续值的处理:决策树需要将连续值离散化,这可能影响性能。
常见的决策树算法:
ID3(Iterative Dichotomiser 3):使用信息增益作为纯度度量。 C4.5:ID3的改进版本,使用增益率作为纯度度量。 CART(Classification And Regression Tree):可以用于分类和回归任务,使用基尼指数作为纯度度量。
决策树是机器学习领域中一种非常强大的工具,它不仅在分类和回归任务中表现出色,还可以用于特征选择和模型解释。
深入解析机器学习中的决策树算法
一、决策树概述
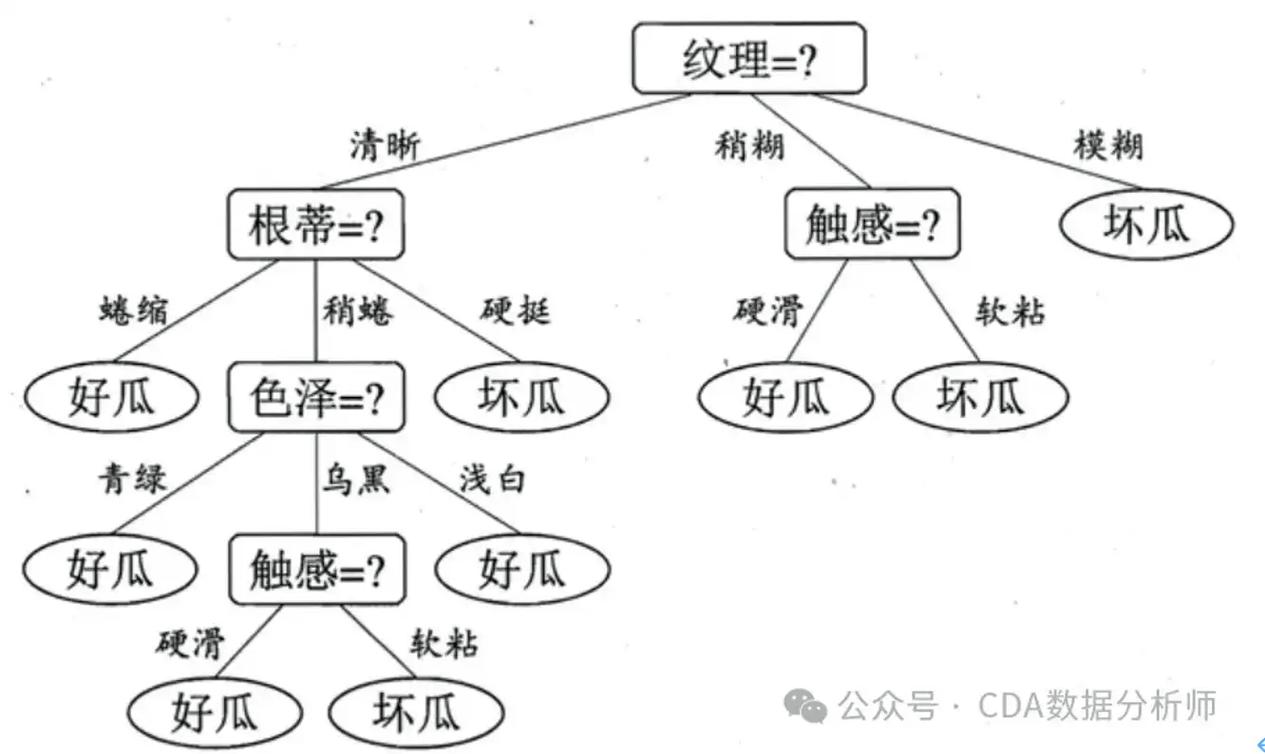
决策树是一种基于树形结构的数据挖掘方法,通过一系列的决策规则(通常是“是/否”问题)来预测目标变量的值。决策树由节点和分支组成,每个节点代表一个特征,每个分支代表一个决策规则。
二、决策树算法原理
决策树算法的核心思想是利用信息增益来选择特征进行分裂。信息增益越大,特征对分类任务的帮助越大。以下是常见的决策树算法及其原理:
1. ID3算法
ID3(Iterative Dichotomiser 3)算法的核心思想是利用信息增益来选择特征进行分裂。信息增益的计算公式如下:
信息增益 = 信息熵(D) - 条件熵(D|A)
其中,信息熵和条件熵的计算公式分别为:
信息熵(D) = -Σk=1K P(k)log2P(k)
条件熵(D|A) = Σk=1K P(k|A)log2P(k|A)
ID3算法采用自顶向下的贪婪搜索策略,递归地构建决策树。
2. C4.5算法
C4.5算法是ID3算法的改进版,它引入了增益率(Gain Ratio)作为划分标准,以解决ID3算法在处理具有大量特征的数据时可能出现的过拟合问题。
增益率 = 信息增益 / 增益率 = 信息增益 / (信息增益 - 信息增益(A))
C4.5算法还引入了剪枝策略,以防止过拟合。
3. CART算法
CART(Classification And Regression Tree)算法是一种基于二叉树的决策树算法,适用于分类和回归任务。CART算法使用基尼系数(Gini Index)作为划分标准,其计算公式如下:
基尼系数 = 1 - Σk=1K P(k)^2
CART算法也支持剪枝策略,以防止过拟合。
三、决策树算法实现
决策树算法的实现通常包括以下步骤:
选择特征:根据信息增益、增益率或基尼系数等标准选择特征。
划分数据:根据选定的特征将数据划分为不同的子集。
递归构建决策树:对每个子集重复步骤1和2,直到满足停止条件。
剪枝:根据剪枝策略对决策树进行剪枝,以防止过拟合。
四、决策树算法应用
金融领域:信用评分、欺诈检测、股票预测等。
医疗领域:疾病诊断、药物推荐、患者预后等。
商业领域:客户细分、市场细分、产品推荐等。
其他领域:文本分类、图像识别、语音识别等。
五、决策树算法优缺点
决策树算法具有以下优点:
可解释性强:决策树的结构直观易懂,便于理解模型的决策过程。
处理非数值数据:决策树可以处理非数值数据,如文本、图像等。
计算效率高:决策树的计算效率较高,适用于大规模数据。
决策树算法也存在以下缺点:
过拟合:决策树容易过拟合,需要采取剪枝策略。
模型复杂度较高:决策树的模型复杂度较高,难以处理复杂问题。
决策树算法作为一种重要的机器学习算法,在分类和回归任务中具有广泛的应用。本文对决策树算法的原理、实现和应用进行了详细解析,希望对读者有所帮助。