机器学习数学原理,机器学习数学原理概述

1. 概率论和统计学：概率论是研究随机事件及其规律性的数学分支。在机器学习中，概率论用于描述数据的不确定性，以及模型的不确定性。统计学则提供了从数据中提取信息的方法，包括估计参数、假设检验和置信区间。

2. 线性代数：线性代数是研究向量空间、线性映射、矩阵和线性方程组的数学分支。在机器学习中，线性代数用于表示和处理数据，例如通过矩阵乘法来计算模型的权重和偏置。

3. 微积分：微积分是研究函数的极限、导数、积分和无穷级数的数学分支。在机器学习中，微积分用于优化模型参数，例如通过梯度下降算法来最小化损失函数。

4. 优化理论：优化理论是研究如何在给定条件下找到最优解的数学分支。在机器学习中，优化理论用于找到模型参数的最优值，以最小化损失函数。

5. 信息论：信息论是研究信息、通信和编码的数学理论。在机器学习中，信息论用于量化数据的不确定性，以及模型预测的不确定性。

6. 图论：图论是研究图（由节点和边组成的数据结构）的数学分支。在机器学习中，图论用于表示和推理数据之间的关系，例如通过图神经网络来处理图结构的数据。

7. 集合论：集合论是研究集合（一组对象）的数学分支。在机器学习中，集合论用于表示和处理数据，例如通过集合操作来处理数据的集合。

8. 数理逻辑：数理逻辑是研究数学中的逻辑和推理的数学分支。在机器学习中，数理逻辑用于表示和推理模型的知识，例如通过逻辑编程来处理模型的知识。

9. 组合数学：组合数学是研究计数问题的数学分支。在机器学习中，组合数学用于解决数据排列、组合和分配问题。

10. 复分析：复分析是研究复数函数的数学分支。在机器学习中，复分析用于处理复数数据，例如通过复数神经网络来处理复数数据。

11. 拓扑学：拓扑学是研究拓扑空间和拓扑映射的数学分支。在机器学习中，拓扑学用于研究数据的几何结构和拓扑性质，例如通过拓扑数据分析来发现数据中的模式。

12. 泛函分析：泛函分析是研究函数空间和泛函的数学分支。在机器学习中，泛函分析用于处理函数的优化问题，例如通过泛函优化来最小化损失函数。

13. 测度论：测度论是研究测度和积分的数学分支。在机器学习中，测度论用于处理数据的不确定性，例如通过测度理论来量化数据的不确定性。

14. 动力系统：动力系统是研究物理系统随时间演化的数学分支。在机器学习中，动力系统用于模拟和学习物理系统的行为，例如通过动力系统模型来预测物理系统的未来状态。

15. 计算几何：计算几何是研究几何问题的算法和理论的数学分支。在机器学习中，计算几何用于处理几何数据，例如通过计算几何算法来处理点云数据。

这些数学概念和原理为机器学习提供了理论基础，并帮助开发新的机器学习算法和模型。

机器学习作为人工智能的一个重要分支，其核心在于通过数学模型从数据中学习规律，并做出预测或决策。理解机器学习的数学原理对于深入掌握和应用机器学习技术至关重要。本文将简要介绍机器学习中的几个关键数学概念和原理。

概率分布：描述随机变量可能取值的概率。

期望值：随机变量的平均值，反映了随机变量的中心趋势。

方差：衡量随机变量取值分散程度的指标。

协方差：衡量两个随机变量之间线性关系强度的指标。

假设检验：基于样本数据对总体参数进行推断的方法。

向量：表示具有大小和方向的量。

矩阵：由一系列数字组成的二维数组，用于表示线性变换。

行列式：矩阵的一个数值，用于描述矩阵的几何性质。

特征值与特征向量：描述矩阵如何改变向量的方向和大小。

正交与单位向量：在空间中具有特定关系的向量。

导数：描述函数在某一点的局部变化率。

微分：函数在某一点的局部变化。

积分：求函数在某区间上的累积变化。

梯度下降：一种优化算法，用于寻找函数的最小值。

梯度下降：通过迭代更新参数，使损失函数最小化。

牛顿法：利用导数和二阶导数来加速优化过程。

拟牛顿法：近似牛顿法，适用于非凸优化问题。

遗传算法：模拟生物进化过程，用于求解复杂优化问题。

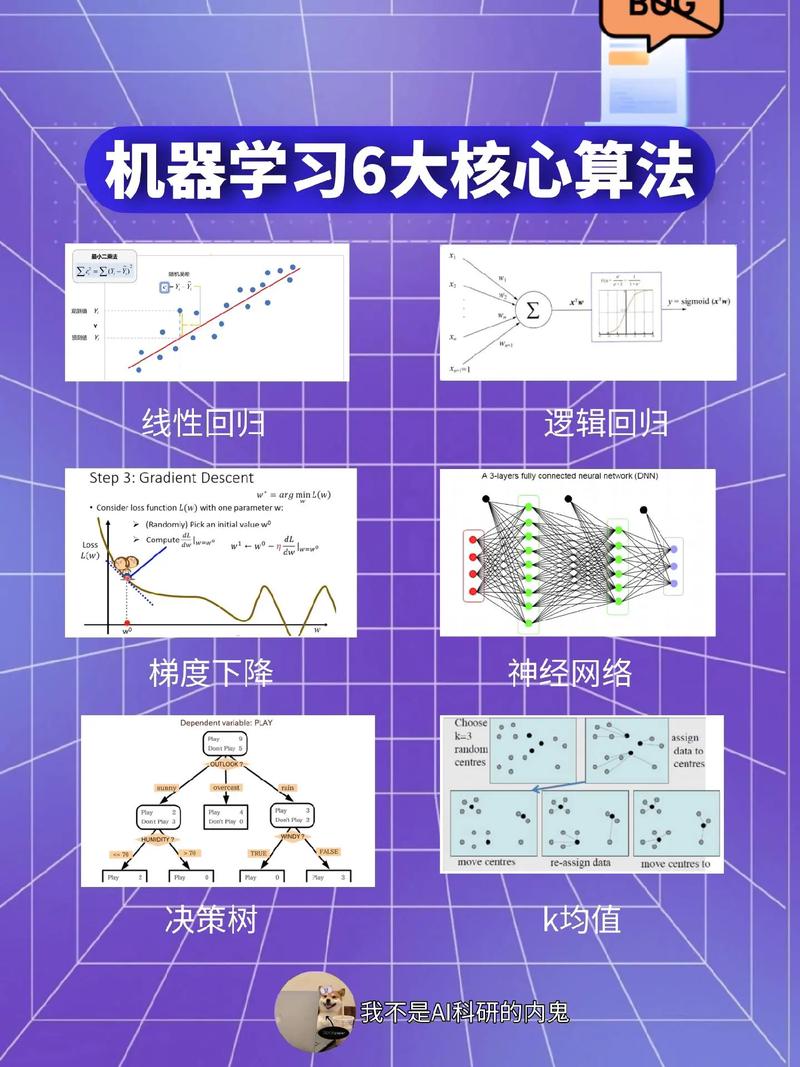
线性回归：通过线性关系预测连续变量。

逻辑回归：通过逻辑函数预测二分类问题。

支持向量机：通过寻找最优超平面进行分类。

神经网络：通过多层非线性变换进行特征提取和分类。

机器学习的数学原理涵盖了概率论、统计学、线性代数、微积分等多个领域。掌握这些数学原理对于深入理解和应用机器学习技术至关重要。本文简要介绍了机器学习中的关键数学概念和原理，旨在为读者提供一个全面的学习路径。