K近邻算法
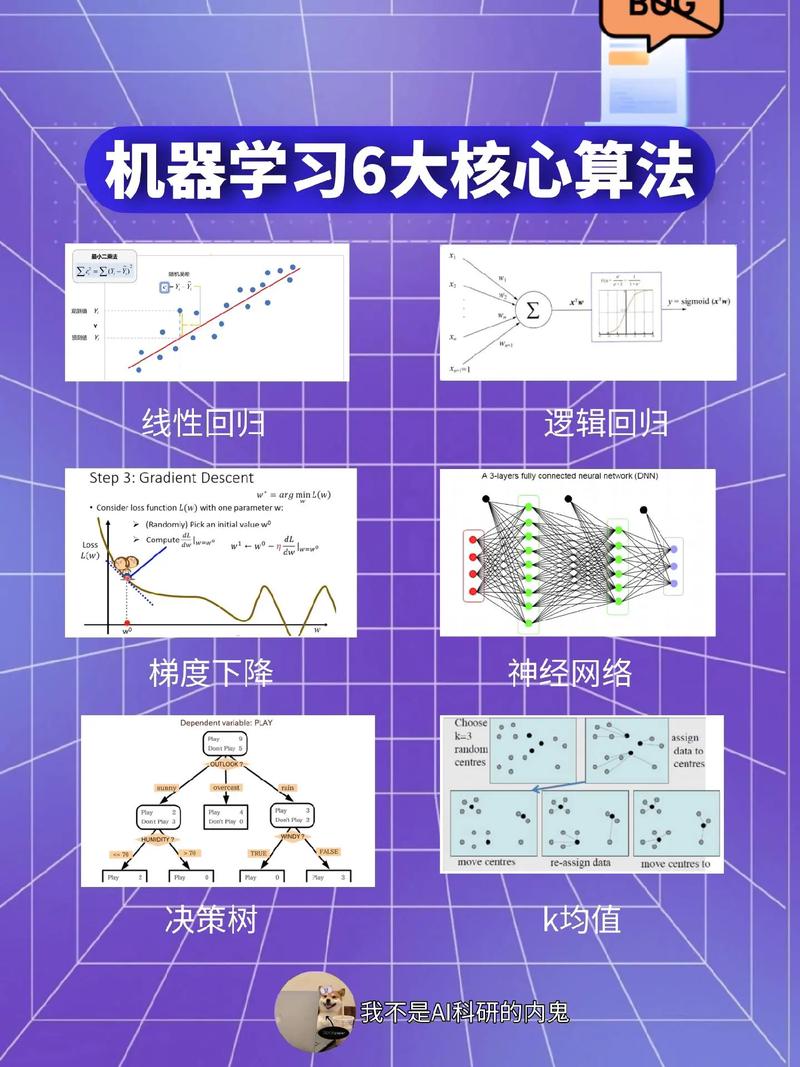
K近邻算法 是一种简单而强大的机器学习算法,用于分类和回归问题。它基于这样一个假设:一个样本的类别由其最近的邻居决定。
KNN 工作原理
1. 距离计算: 对于一个新的样本,计算其与训练集中所有样本的距离。2. 选择邻居: 从训练集中选择与该样本距离最近的 K 个样本作为邻居。3. 投票/平均: 根据邻居的类别进行投票,选择得票最多的类别作为新样本的类别(分类问题)。对于回归问题,则计算邻居的输出值的平均值作为新样本的预测值。
KNN 优缺点
优点:
简单易实现 无需进行参数调整 对异常值鲁棒
缺点:
计算量大,尤其是 K 值较大时 需要选择合适的 K 值 对噪声敏感
KNN 应用
KNN 算法广泛应用于各种领域,例如:
图像识别 文本分类 医疗诊断 推荐系统
KNN 实现示例
以下是一个使用 Python 实现的 KNN 算法示例:
```pythonfrom collections import Counterimport numpy as np
def knn: KNN 算法实现 计算距离 distances = np.sqrt2, axis=1qwe2qwe2 选择最近的 K 个邻居 neighbors = np.argsort 获取邻居的类别 neighbor_labels = y_train 投票 label_counts = Counter 返回得票最多的类别 return label_counts.most_common```
KNN 算法是一种简单而强大的机器学习算法,适用于各种分类和回归问题。尽管它存在一些缺点,但在很多情况下仍然是一个非常有效的选择。
深入解析K近邻算法(KNN)在机器学习中的应用
一、K近邻算法简介

K近邻算法(K-Nearest Neighbors,简称KNN)是一种基于实例的监督学习算法。它通过比较待分类数据点与训练集中所有数据点的距离,根据距离最近的K个数据点的类别来预测待分类数据点的类别。
二、K近邻算法的工作原理
1. 计算距离:首先,我们需要计算待分类数据点与训练集中所有数据点之间的距离。常用的距离度量方法有欧氏距离、曼哈顿距离、切比雪夫距离等。
2. 排序:将计算出的距离按照从小到大的顺序进行排序。
3. 选择K个最近邻:从排序后的距离中选取距离最近的K个数据点。
4. 分类决策:统计这K个最近邻数据点的类别,并选择出现频率最高的类别作为待分类数据点的预测类别。
三、K近邻算法的距离度量
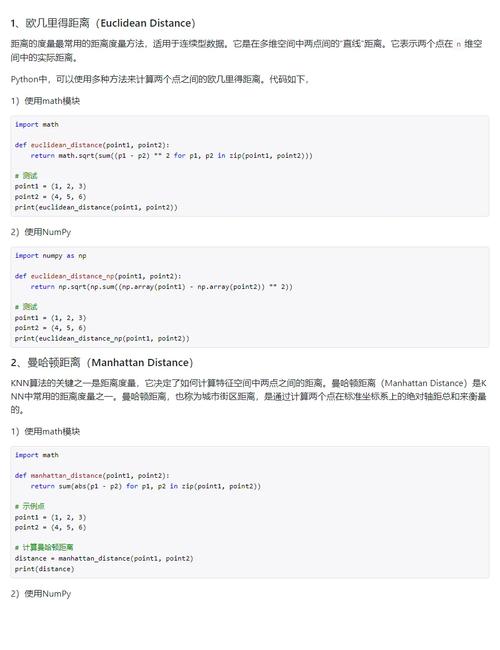
1. 欧氏距离:欧氏距离是空间中两点之间的直线距离,适用于多维空间。其计算公式为:d(x, y) = √(Σ(xi - yi)^2),其中xi和yi分别表示两个数据点在第i维上的值。
2. 曼哈顿距离:曼哈顿距离是空间中两点之间的直线距离,适用于一维空间。其计算公式为:d(x, y) = Σ|xi - yi|,其中xi和yi分别表示两个数据点在第i维上的值。
3. 切比雪夫距离:切比雪夫距离是空间中两点之间的最大距离,适用于多维空间。其计算公式为:d(x, y) = max(|xi - yi|),其中xi和yi分别表示两个数据点在第i维上的值。
四、K近邻算法的K值选择
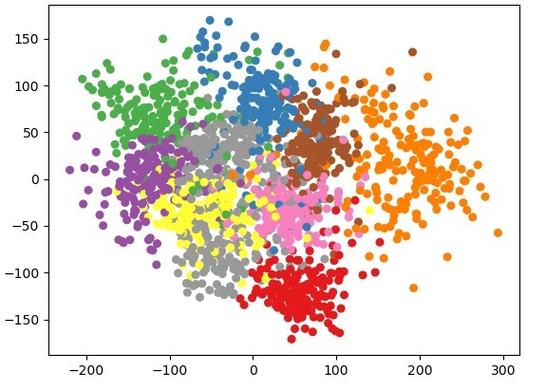
1. 经验选择法:根据经验选择一个合适的K值,如K=3、5、7等。
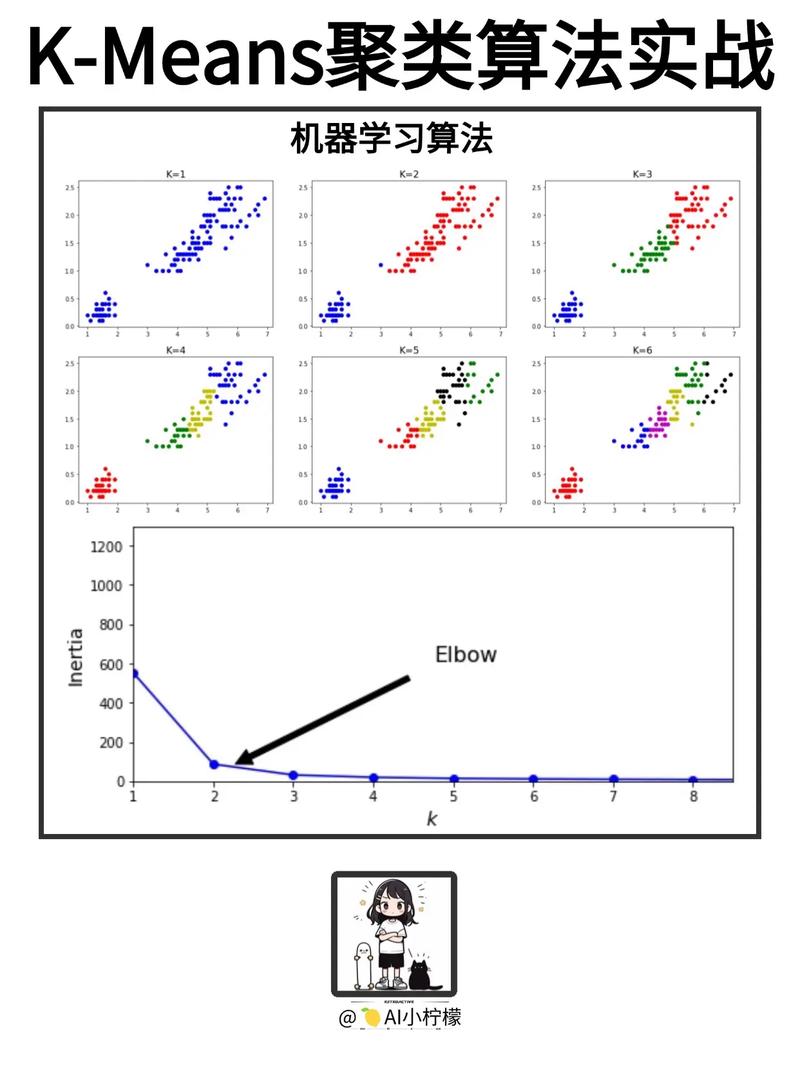
2. 肘部法:通过绘制K值与模型准确率之间的关系图,找到准确率发生显著变化的点,该点附近的K值可以作为参考。
3. 交叉验证:使用交叉验证方法,通过调整K值,找到最优的K值。
五、K近邻算法的优缺点
1. 优点:
(1)简单易懂,易于实现。
(2)适用于各种类型的数据,包括数值型和类别型数据。
(3)不需要复杂的模型训练过程。
2. 缺点:
(1)计算量大,尤其是当数据集较大时。
(2)对噪声数据敏感,容易受到异常值的影响。
(3)K值的选择对分类结果有较大影响。
六、K近邻算法的应用场景
1. 图像识别:K近邻算法可以用于图像识别任务,如人脸识别、物体识别等。
2. 推荐系统:K近邻算法可以用于推荐系统,如电影推荐、商品推荐等。
3. 医疗诊断:K近邻算法可以用于医疗诊断,如疾病预测、药物推荐等。
K近邻算法是一种简单易懂、易于实现的机器学习算法。它在各种应用场景中都有广泛的应用。K近邻算法也存在一些缺点,如计算量大、对噪声数据敏感等。在实际应用中,我们需要根据具体问题选择合适的距离度量方法、K值选择方法,并注意处理噪声数据。