-
花漫画
你知道吗?在这个五彩斑斓的网络世界里,有一种独特的艺术形式,它不仅让人笑得前俯后仰,还能让人沉浸在花的世界里流连忘返。这就是——...
2025-12-07 46 -
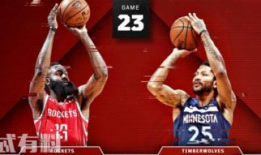
91直播nba回放,重温赛场激情与精彩对决
篮球迷们,是不是最近错过了精彩的NBA比赛,但又不想错过每一个精彩瞬间?别担心,今天我要给你揭秘一个宝藏网站——91直播NBA回...
2025-12-07 44 -
娱乐圈吃瓜背景图女星,揭秘“吃瓜图”背后的明星故事
娱乐圈的瓜,你吃了吗?在这个信息爆炸的时代,娱乐圈的瓜可谓是层出不穷,让人应接不暇。今天,就让我带你一起走进娱乐圈的吃瓜世界,看...
2025-12-06 44 -
漫画街道,漫画中的街道风情
你有没有想过,那些充满色彩和故事的街道,其实就像一本本漫画书?走在这样的街道上,仿佛每一步都能踏进一个全新的故事里。今天,就让我...
2025-12-06 44 -
逆后宫漫画,众男爱一女,浪漫纠葛的甜蜜漩涡
你有没有听说过那种让人心跳加速、脸红心跳的漫画类型?没错,就是逆后宫漫画!这种类型的漫画可是近年来在二次元世界里掀起了一股热潮。...
2025-12-06 45 -
逆水寒91直播,揭秘古风江湖的奇幻之旅
你有没有听说过逆水寒91直播?最近这可是游戏圈里的一股热潮呢!想象夜幕低垂,你坐在电脑前,屏幕上那个江湖世界正热闹非凡。没错,这...
2025-12-06 45 -
娱乐圈吃瓜爆料电影有哪些,那些被吃瓜爆料的电影幕后故事
娱乐圈吃瓜爆料电影:揭秘那些你不知道的幕后故事亲爱的读者们,你是否也和我一样,对娱乐圈的八卦新闻充满好奇?那些明星们的幕后故事,...
2025-12-06 45 -
陈赫娱乐圈吃瓜事件视频,揭秘吃瓜视频背后的真相
最近娱乐圈可是热闹非凡呢!陈赫这个名字再次成为了大家热议的焦点。这不,一段关于他的吃瓜视频在网上疯传,引发了无数网友的热议。今天...
2025-12-06 42 -
白狼漫画,探寻狼族传奇,揭秘神秘力量
亲爱的读者们,你是否曾在某个午后,手捧漫画,沉浸在奇幻的世界中?今天,我要和你聊聊一本特别有趣的漫画——《白狼》。一、邂逅《白狼...
2025-12-06 55 -
娱乐圈吃瓜爆料一更到底,一网打尽明星秘闻,揭秘幕后真相!
娱乐圈吃瓜爆料一更到底亲爱的读者们,你们准备好迎接娱乐圈的最新爆料了吗?今天,我要带你们深入挖掘那些隐藏在光鲜亮丽背后的秘密。娱...
2025-12-06 56