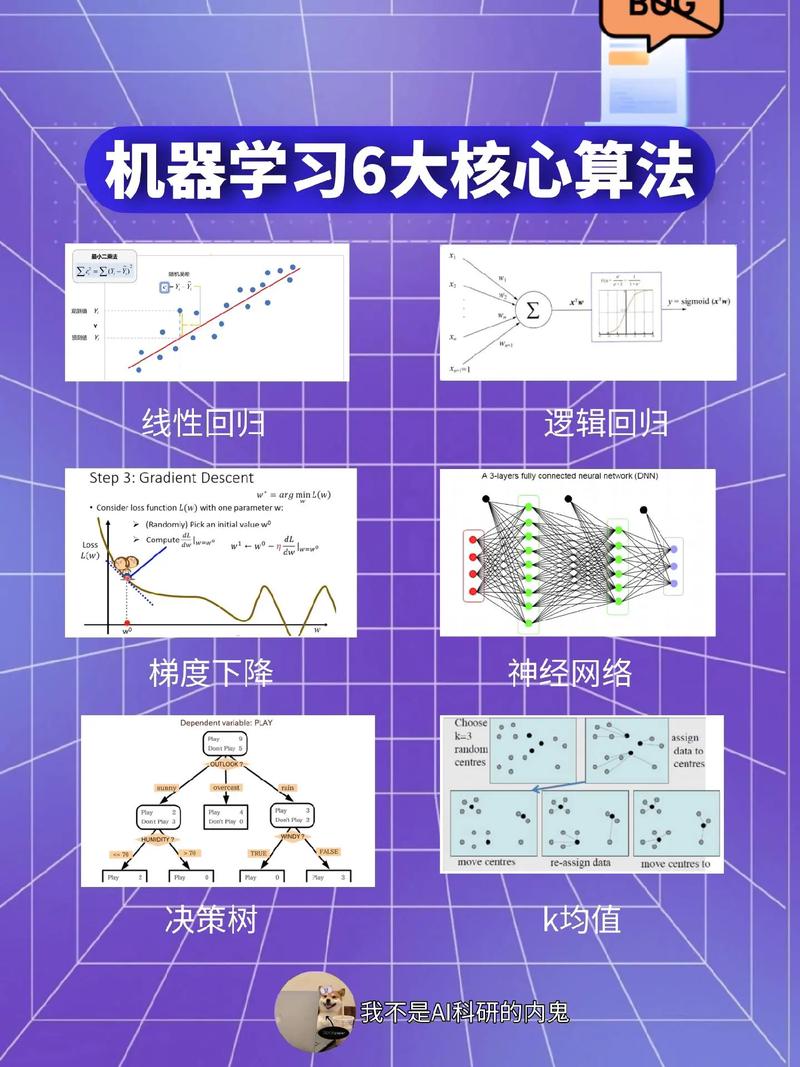
聚类是一种无监督学习的方法,主要用于将数据集分为不同的组或“簇”,使得同一簇内的数据点彼此相似,而不同簇的数据点则彼此不相似。这种方法在很多领域都有应用,比如市场细分、客户关系管理、图像处理和社交网络分析等。
在聚类算法中,常见的有K均值聚类、层次聚类、DBSCAN等。K均值聚类是一种基于距离的算法,它将数据集分为K个簇,每个簇由一个中心点代表。层次聚类则是一种基于树结构的算法,它将数据集逐步合并或分裂成不同的簇。DBSCAN是一种基于密度的算法,它可以将具有足够高密度的区域划分为簇,而将低密度的区域视为噪声。
聚类算法的选择取决于数据的特点和聚类目标。在实际应用中,通常需要通过实验和调整参数来找到最佳的聚类方案。
聚类机器学习:探索数据内在结构的新方法
什么是聚类机器学习

聚类算法概述
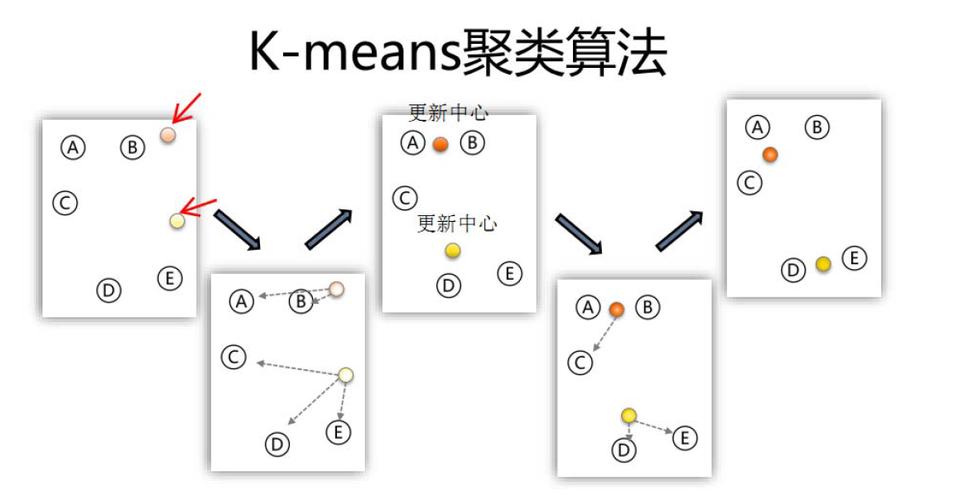
K-Means算法:基于距离的聚类算法,通过迭代计算簇中心,将数据点分配到最近的簇中心。
层次聚类:通过合并或分裂簇来构建一个树状结构,称为聚类树或谱系图。
DBSCAN算法:基于密度的聚类算法,可以识别任意形状的簇,并能够处理噪声和异常值。
谱聚类:通过分析数据点的相似性矩阵来识别簇,适用于高维数据。
聚类算法的选择
数据类型:不同的聚类算法适用于不同类型的数据,例如,K-Means适用于数值型数据,而层次聚类适用于任何类型的数据。
数据规模:对于大规模数据集,一些算法可能比其他算法更高效。
簇的形状:不同的算法对簇的形状有不同的假设,例如,K-Means假设簇是球形的,而DBSCAN可以识别任意形状的簇。
噪声和异常值:一些算法对噪声和异常值更鲁棒,例如,DBSCAN可以处理噪声和异常值。
聚类结果的评估

轮廓系数:衡量簇内数据点之间的相似性和簇间数据点之间的差异性。
Calinski-Harabasz指数:衡量簇内数据点之间的相似性和簇间数据点之间的差异性,但比轮廓系数更敏感于簇的大小。
Davies-Bouldin指数:衡量簇内数据点之间的相似性和簇间数据点之间的差异性,但比Calinski-Harabasz指数更敏感于簇的形状。
聚类在实际应用中的案例
市场细分:通过聚类分析,企业可以将客户分为不同的群体,以便更好地了解客户需求,制定营销策略。
图像识别:聚类算法可以用于图像识别任务,例如,将图像中的对象分为不同的类别。
社交网络分析:聚类算法可以用于分析社交网络中的用户关系,识别社区和子群。
聚类机器学习是一种强大的工具,可以帮助我们探索数据中的内在结构。通过选择合适的算法、评估聚类结果,并在实际应用中应用聚类技术,我们可以从数据中获得有价值的见解。