机器学习 svm,深入解析支持向量机（SVM）在机器学习中的应用

SVM（支持向量机）是一种强大的机器学习算法，广泛应用于分类和回归问题。以下是SVM的一些基本概念和原理：

1. 基本思想：SVM的目标是在特征空间中找到一个超平面，这个超平面可以将不同类别的数据点尽可能分开。这个超平面称为“最优超平面”，它应该位于两类数据点之间，并且距离两类数据点的距离最大化。

2. 线性SVM：当数据是线性可分时，可以使用线性SVM来找到最优超平面。线性SVM通过最大化两类数据点之间的间隔来实现这一点。

3. 非线性SVM：当数据不是线性可分时，可以使用非线性SVM来找到最优超平面。非线性SVM通过使用核函数将数据映射到高维空间，从而使得数据变得线性可分。

4. 核函数：核函数是SVM中用于将数据映射到高维空间的函数。常用的核函数包括线性核、多项式核、径向基函数（RBF）核等。

5. 软间隔：在实际应用中，数据往往不是完全线性可分的。为了解决这个问题，SVM引入了“软间隔”的概念。软间隔允许一些数据点位于超平面的错误侧，但会对这些数据点进行惩罚。

6. 参数调整：SVM的性能壬能准确地预测连续的输出值。

9. SVM的优缺点：SVM的优点包括强大的泛化能力、对异常值不敏感等。SVM的缺点包括训练时间较长、对参数选择敏感等。

10. 应用领域：SVM在许多领域都有应用，如文本分类、图像识别、生物信息学等。

支持向量机（Support Vector Machine，简称SVM）是一种强大的监督学习算法，广泛应用于分类和回归问题。本文将深入解析SVM的原理、应用场景以及优缺点，帮助读者更好地理解这一机器学习算法。

支持向量机的基本思想是通过构造一个超平面（Hyperplane）来将不同类别的数据点分开，使得类之间的间隔最大化。换句话说，SVM试图找到一个最优的决策边界，使得不同类别的点在该边界的两侧有最大的间隔，从而提高分类的准确性和泛化能力。

SVM的数学原理基于优化问题，通过最大化分类间隔来实现分类。以下将通过数学推导详细介绍其基本原理。

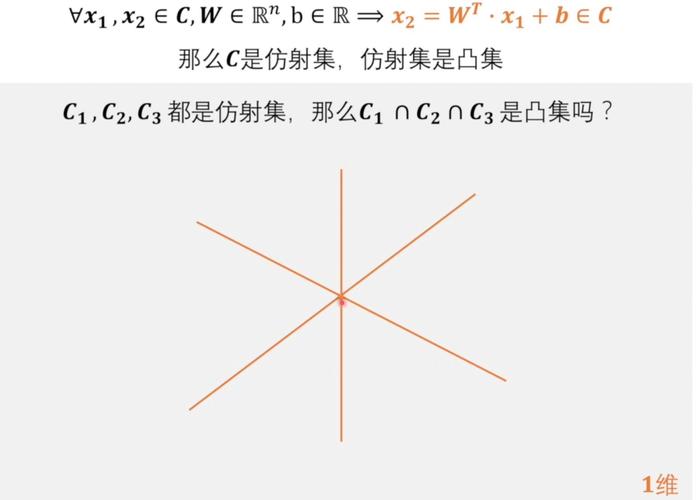
为了找到最优的超平面，我们需要解决一个最优化问题。具体来说，我们需要最大化以下目标函数：

最大化间隔：maximize (1/2) ||w||^2，其中 ||w|| 表示向量 w 的欧几里得范数。

由于目标函数中存在约束条件，我们需要使用拉格朗日对偶问题来求解。拉格朗日对偶问题将原始问题转化为一个无约束的优化问题，从而更容易求解。

当数据不可线性分割时，SVM通过核技巧将数据映射到更高维的空间，使得原本不可分的情况变得可分。常用的核函数包括线性核、多项式核、高斯核（RBF）和Sigmoid核等。

SVM具有良好的泛化能力，在许多实际问题中表现出色。以下列举一些SVM的应用场景：

垃圾邮件过滤、情感分析等。

手写数字识别、面部识别等。

癌症诊断、蛋白质结构预测等。

信用评分、股票市场预测等。

疾病分类等。

4.1 优点

1. 适合高维数据：在高维数据中仍表现良好。

2. 非线性处理能力强：通过核技巧解决非线性问题。

3. 泛化能力强：通过最大化间隔提高模型的鲁棒性。

4.2 缺点

1. 计算复杂度高：在处理大规模数据集时，SVM的计算复杂度较高。

2. 对参数敏感：SVM的参数较多，需要根据具体问题进行调整。

3. 不适用于大规模数据集：当数据集规模较大时，SVM的训练和预测速度较慢。

支持向量机（SVM）是一种强大的监督学习算法，在许多实际问题中表现出色。本文从基本概念、数学原理、应用场景、优缺点等方面对SVM进行了深入解析，希望对读者有所帮助。