机器学习是人工智能的一个重要分支,它使计算机系统能够通过数据学习并做出决策或预测。机器学习的数学基础涵盖了多种数学学科,包括但不限于线性代数、概率论、统计学、优化理论和信息论。下面简要介绍这些基础学科在机器学习中的应用:
1. 线性代数: 向量和矩阵:在机器学习中,数据通常表示为向量或矩阵。例如,在图像识别中,图像可以表示为一个向量或矩阵,其中每个元素代表图像的一个像素。 特征空间:线性代数帮助我们将数据映射到高维空间,以便更好地理解和分析数据。 线性变换:线性代数中的线性变换(如旋转、缩放和平移)用于数据预处理和特征提取。
2. 概率论: 概率分布:概率论提供了一种量化不确定性的方法。在机器学习中,概率分布用于描述数据分布和模型的不确定性。 贝叶斯定理:贝叶斯定理是概率论中的一个重要概念,它描述了如何根据新证据更新先验概率。在机器学习中,贝叶斯定理用于贝叶斯分类器和贝叶斯网络。
3. 统计学: 估计和假设检验:统计学提供了一种从样本数据推断总体参数的方法。在机器学习中,统计学用于模型参数的估计和假设检验。 回归分析:回归分析是一种统计方法,用于建立变量之间的关系。在机器学习中,回归分析用于预测和分析数据。
4. 优化理论: 梯度下降:优化理论中的梯度下降是一种常用的优化算法,用于找到函数的局部最小值。在机器学习中,梯度下降用于训练模型参数,以最小化损失函数。 拟合和正则化:优化理论还用于模型的拟合和正则化,以避免过拟合和提高模型的泛化能力。
5. 信息论: 信息熵:信息论中的信息熵用于衡量数据的不确定性。在机器学习中,信息熵用于特征选择和模型评估。 交叉熵:交叉熵是信息论中的一个重要概念,用于衡量两个概率分布之间的差异。在机器学习中,交叉熵用于损失函数的计算。
这些数学学科为机器学习提供了理论基础和工具,使机器学习能够有效地处理和分析数据,并做出准确的预测和决策。掌握这些数学基础对于深入理解机器学习算法和模型至关重要。
一、线性代数

线性代数是机器学习数学基础的核心部分,它主要研究向量、矩阵以及它们之间的运算。以下是线性代数在机器学习中的几个关键概念:
1. 向量与矩阵
向量是具有大小和方向的量,在机器学习中常用以表示数据。矩阵是由多个向量组成的二维数组,可以用来表示数据集和模型参数。
2. 矩阵运算
矩阵运算包括矩阵加法、矩阵乘法、转置、逆矩阵等。这些运算在机器学习中用于处理数据、计算模型参数等。
3. 特征值与特征向量

特征值和特征向量是矩阵理论中的重要概念,它们在降维、特征选择等方面有广泛应用。
二、概率论与数理统计

概率论与数理统计是机器学习中的另一个重要数学基础,它们为机器学习提供了理论基础。以下是概率论与数理统计在机器学习中的几个关键概念:
1. 概率与随机变量

概率是描述随机事件发生可能性的度量。随机变量是取值不确定的变量,可以是离散的也可以是连续的。
2. 概率分布

概率分布描述了随机变量取值的概率分布情况,常见的概率分布有正态分布、伯努利分布等。
3. 期望与方差

期望是随机变量的平均值,方差是随机变量取值与其期望之差的平方的平均值。它们在评估模型性能、优化模型参数等方面有重要作用。
三、微积分

微积分是研究函数、极限、导数、积分等概念的数学分支。在机器学习中,微积分主要用于优化算法、求解最优化问题等。以下是微积分在机器学习中的几个关键概念:
1. 极限与导数

极限是函数在某一点附近取值的趋势,导数是函数在某一点处的变化率。它们在优化算法中用于求解最优化问题。
2. 积分
积分是求函数在某区间上的累积值,它在机器学习中用于计算概率密度函数、求解积分方程等。
四、优化算法
优化算法是机器学习中的核心内容,它用于求解最优化问题,从而找到最优的模型参数。以下是几种常见的优化算法:
1. 梯度下降法
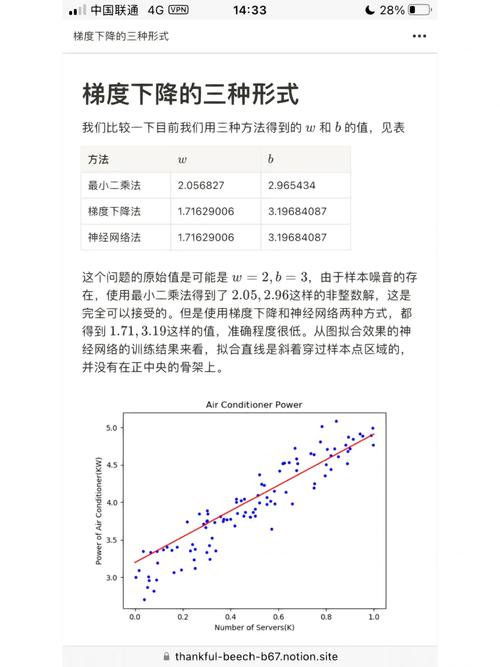
梯度下降法是一种常用的优化算法,它通过迭代更新模型参数,使损失函数最小化。
2. 随机梯度下降法(SGD)
随机梯度下降法是梯度下降法的一种改进,它通过随机选择样本进行迭代,提高了算法的收敛速度。
3. 牛顿法
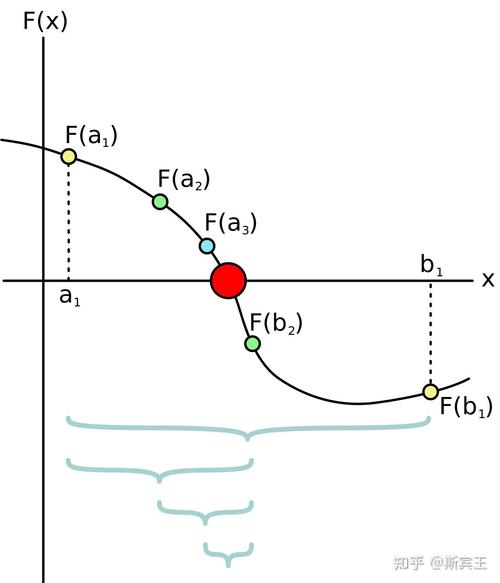
牛顿法是一种基于二次函数的优化算法,它通过迭代更新模型参数,使损失函数的二阶导数最小化。
机器学习数学基础是理解和应用机器学习算法的关键。本文介绍了线性代数、概率论与数理统计、微积分以及优化算法等数学基础,为读者深入学习机器学习提供了必要的理论基础。掌握这些数学知识,将有助于读者在机器学习领域取得更好的成果。