admin
59
0
娱乐圈,这个光鲜亮丽的舞台,总是充满了各种八卦和话题。而在这片热闹的海洋中,有一群特殊的“观众”——吃瓜群众。他们热衷于在群聊中分享、讨论、猜测,仿佛置身于娱乐圈的幕后,享受着这场视觉盛宴。今天,就让我们一起走进娱乐圈吃瓜群众的群聊,看看他们是如何“吃瓜”的。瓜田里的“侦探”在娱乐圈吃瓜群众的群聊里,总有一些人被称为“侦探”。他们善于挖掘各种线索,从明星的微博、朋友圈、机场照中寻找蛛丝马迹。比如,某位明星突然在微博上晒出一张与神秘人物的合影,吃瓜群众们就会...
admin
57
0
亲爱的读者们,今天我要给你带来一个超级劲爆的消息,保证让你眼睛一亮,嘴巴一咧,就差没喊出“吃瓜酱出远门”了!没错,就是那个我们每天都能在屏幕前看到,笑料百出、八卦满天飞的小可爱——娱乐吃瓜酱,竟然要踏出家门,去探索未知的世界啦!快来跟我一起,从多个角度来了解一下这个让人兴奋的消息吧!一、吃瓜酱的“远门”之旅首先,让我们来了解一下吃瓜酱这次出远门的背景。据可靠消息,这次吃瓜酱的远门之旅是为了参加一个国际娱乐论坛,与全球的娱乐达人交流心得,共同探讨娱乐产业的发...
admin
53
0
亲爱的读者们,是不是又到了周末,心情是不是已经迫不及待地想要放松一下呢?今天,就让我带你走进一个热闹非凡的聊天世界,让我们一起聊聊那些让人津津乐道的娱乐吃瓜话题吧!娱乐圈的“瓜”总是那么新鲜娱乐圈,一个充满话题的地方,每天都有新鲜事发生。比如,最近某位明星的恋情曝光,立刻成为了大家热议的焦点。有人猜测他们是不是已经秘密领证,有人则调侃他们的恋情能否经受住时间的考验。这种八卦话题,总是能让人忍不住想要一探究竟。综艺节目里的“笑料”不断综艺节目,作为娱乐圈的另...
admin
61
0
你有没有发现,最近大学校园里的小道消息可是越来越热闹了?那些曾经只在电视剧里出现的“吃瓜群众”,现在竟然成了我们身边最活跃的一群人。他们,就是那些热衷于“娱乐吃瓜酱”的大学生。今天,就让我带你一起走进他们的世界,看看他们是如何在忙碌的学习生活中,找到属于自己的乐趣。一、校园八卦,无处不在走进大学校园,你总能听到各种八卦消息。这些消息,有的是关于明星的,有的是关于老师的,还有的是关于同学的。而这些消息的传播者,往往就是那些热衷于“娱乐吃瓜酱”的大学生。他们就...
admin
59
0
最近娱乐圈可是热闹非凡呢!乔欣和杨紫这对好姐妹,竟然也被卷入了一场吃瓜大戏。咱们就来聊聊这个话题,看看她们是如何在娱乐圈中成为焦点,又是如何应对这场突如其来的风波。瓜田李下,乔欣杨紫成焦点话说,乔欣和杨紫,一个是清新脱俗的氧气女神,一个是古灵精怪的国民闺女。两人自出道以来,就备受粉丝喜爱。这不,最近她们竟然被网友挖出了一些“秘密”,一时间,吃瓜群众纷纷围观。原来,乔欣和杨紫在私下里可是好得不得了,两人经常一起逛街、吃饭,甚至还被拍到一起看电影。这样的友情,...
admin
160
0
亲爱的读者们,你是不是也和我一样,每天在互联网上闲逛,寻找那些让人心跳加速的娱乐八卦呢?没错,今天我要带你走进一个神秘的世界,一个充满新鲜热辣的爆料入口——娱乐吃瓜圈。准备好了吗?让我们一起揭开这个神秘世界的面纱吧!揭秘娱乐圈的“秘密花园”首先,你得知道,娱乐圈就像一个巨大的“秘密花园”,里面藏满了各种鲜为人知的秘密。而这些秘密,往往就是那些让人津津乐道的吃瓜素材。那么,如何才能找到这个“秘密花园”的入口呢?1. 关注各大娱乐新闻网站:像腾讯娱乐、新浪娱乐...
admin
159
0
你有没有发现最近手机上多了一个神奇的小玩意儿?没错,就是那个让你一打开就能看到各种娱乐八卦、明星动态的小程序——娱乐吃瓜入口!今天,就让我带你一起探索这个小程序的奥秘,看看它到底有什么魅力,让你忍不住下载安装。一、轻松一搜,海量信息尽在掌握还记得以前追星时,为了找到最新的明星动态,你需要在各大网站、社交媒体上翻来覆去地找吗?现在,有了娱乐吃瓜入口,这一切都变得简单了。只需在搜索框里输入你想了解的明星名字或者关键词,瞬间就能找到相关的新闻、图片、视频等内容。...
admin
187
0
你知道吗?娱乐圈这个大染缸里,每天都有新鲜事儿冒出来,让人眼花缭乱。而我,这个一线吃瓜群众,就像海底的月亮,静静地观察着这一切,今天就来给你揭秘娱乐圈那些不为人知的秘密。海底见月:我的娱乐圈观察日记自从我踏入这个圈子,我就立志要成为一名吃瓜群众中的佼佼者。每天,我都会像海绵一样吸收各种八卦,然后像侦探一样分析其中的蛛丝马迹。今天,就让我带你一起看看娱乐圈的月亮。一、明星们的“月圆之夜”你知道吗,明星们也有月圆之夜?没错,那就是他们的生日。每当这个时候,粉丝...
admin
159
0
你有没有发现,娱乐圈就像一个大瓜田,每天都有新鲜事儿冒出来,让人忍不住想要一探究竟?今天,就让我带你走进这个热闹非凡的瓜田,一起揭开娱乐圈那些不为人知的秘密吧!一、明星们的“瓜皮”日常你知道吗,明星们的生活其实并不像你想象中那么光鲜亮丽。他们也有自己的喜怒哀乐,也有那些让人捧腹大笑的瞬间。1. 拍戏现场的小趣事在拍摄现场,明星们也会遇到各种意想不到的趣事。比如,某位明星在拍摄一场哭戏时,竟然笑场了,场面一度尴尬。还有一次,某位明星在拍摄一场打戏时,不小心把...
admin
158
0
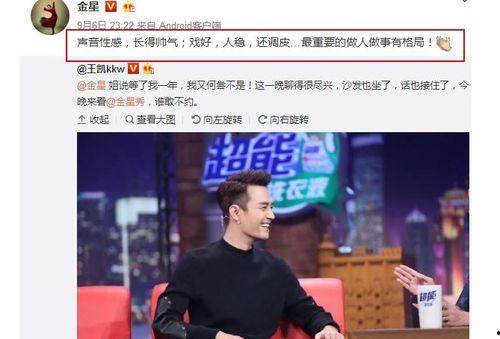
娱乐圈的“吃瓜群众”们,你们有没有注意到,最近李现这个名字在网络上可是火得一塌糊涂呢!今天,就让我带你一起深入挖掘一下这位当红炸子鸡的“吃瓜元素表”。一、颜值担当,李现的“吃瓜”之路李现,一个阳光帅气的小伙子,凭借在《亲爱的,热爱的》中饰演韩商言一角,迅速走红。他的颜值和演技都得到了观众们的认可,成为了娱乐圈的“吃瓜”焦点。1. 颜值爆表,李现的“吃瓜”魅力李现的颜值可以说是娱乐圈的一股清流,他的五官精致,笑容阳光,给人一种温暖的感觉。在《亲爱的,热爱的》...